SCHULE ONLINE 04/05 - MATHE 4A - LE02
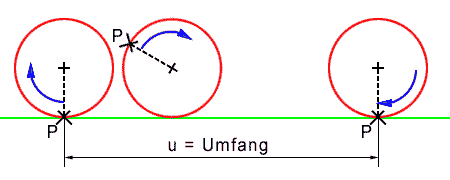SCHULE ONLINE 04/05 MATHE 4A HOME	LE02: Umfang des Kreises   Viele Gegenstände im alltäglichen Leben haben eine kreisförmige Grundfläche! Wiederholung zum Kreis!   Nimm 2 Gegenstände mit kreisförmiger Grundfläche (verschieden groß) und bestimme durch Abrollen auf einem Blatt Papier ihren Umfang. Schreib den Durchmesser und den Umfang dieser beiden Gegenstände auf! Je größer der Durchmesser eines Kreises, umso größer ist der Umfang! Berechne für beide Gegenstände u : d ! Vergleiche nun deine Messungen mit denen deiner Mitschüler/innen! Was fällt euch auf? ??? Berühmten Mathematikern ist es gelungen, diese Zahl u : d genauer zu berechnen. Sie wird Pi genannt. p = 3,14159 Umfang des Kreises: oder Berechne nun den Umfang deiner beiden Gegenstände mithilfe der Formel! p findest du auch auf deinem Taschenrechner! Vom Punkt A kannst du auf drei verschiedenen Wegen zum Punkt B gelangen! Welcher der drei Wege ist der längste? Welcher der kürzeste Weg? Schätze und rechne erst dann! 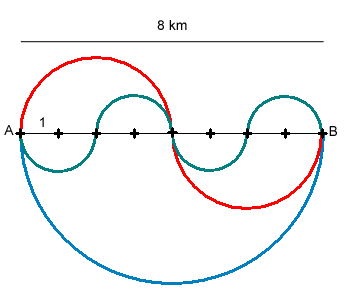Lösung   Die folgende Abbildung zeigt zwei von insgesamt acht Laufbahnen eines Stadions. Die gedachte Lauflinie (strichliert, in der Mitte jeder Bahn) ist ebenfalls eingezeichnet. Der Abstand der Lauflinie in der innersten Bahn beträgt 30cm, bei allen weiteren Bahnen beträgt der Abstand 20cm. 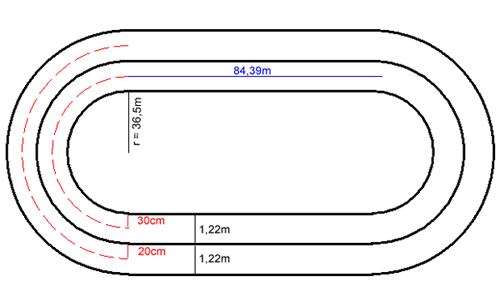Fertige selbst eine entsprechende Zeichnung an! Wie lang ist die gedachte Lauflinie der ersten Bahn? Wie lang ist die gedachte Lauflinie der zweiten Bahn? Wie muss die Startaufstellung sein, damit der erste und zweite Läufer eine gleich lange Strecke (400m) haben? Lösung   Die Zahl p ist eine unendliche, nicht periodische Dezimalzahl! Sie ist eine irrationale Zahl! Mehr zur Geschichte dieser Zahl erfährst du auf folgenden Webseiten: http://www.uni-leipzig.de/~sma/pi_einfuehrung/geschichte.html http://www.bezendingen.ch/Pi/GeschichtederZahlPi/GeschPi.html http://www.eag.aa.schule-bw.de/PROJEKTE/MUW/PI/gesch.htm http://pi314.at/math/geschichte.html